1. 가용응력장, 가용속도장 admissible stress field, sdmissible velocity field

   개요

 소성론에서 상,하계 정리는 1950년대에 브라운대학에서 Drucker 등에 의하여 확립되었는데, 상,하계 정리를 조합한 기본적인 개념이 가용응력장(admissible stress field)과 가용속도장(admissible velocity field)이다.

   가. 가용응력장(可容應力場)

 가용응력장은 일반적으로 정적인 힘의 조합으로서 다음의 3가지 조건을 만족하는 응력계를 말한다.

1) 조합조건을 만족한다.

2) 경계조건을 만족한다.

3) 항복조건을 만족하거나 그 이하이다.

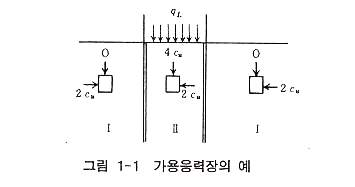
그림 1-1 은 흙의 자중을 무시할 경우 대상기초의 지지력 문제에 대한 가용응력장의 예인데, 그림에서 2중선으로 나타낸 것은 응력의 불연속선으로서 흙은 Tresca의 항복조건을 만족하고, 흙의 강도는 비배수강도(Cu)의 경우이다.

영역 Ⅰ, Ⅱ 모두 최대, 최소 주응력이 2 Cu 로서 항복조건을 만족하며, 또한 응력의 불연속선에 수직인 응력은 평형을 이루고 있다. 흙의 자중을 무시하므로 지지력 q 는 4 Cu 와 같다.

정해값은 금속소성론의 결과에서 (π+2)Cu ≒ 5.14 Cu 이므로 이 가용응력장은 하계값이 주어지는데, 이것을 일반적으로 증명한 것이 하계정리이며, 가용응력장에서 구한 응력은 지지력문제 등 광의의 수동토압 문제로서는 정해갑을 넘지 않는 하계값이 주어지는 것으로 알려져 있다.

일반적으로 정해값에 가까운 가용응력장은 구하기가 상당히 어려운데 눈으로 보지 않는 개념으로서 응력계를 고려하는 것은 그리 단순하지 않기 때문이다.

그래서, 계산기를 사용하여 수치계산으로 정해값에 가까운 가용응력장을 구하는 경우도 있다. 라이스머(Lysmet), 파스터(Paster) 등의 연구가 그 예이다.

이 양자 모두 기본적으로 1), 2), 3),의 조건을 만족하는 최대의 응력계를 구하는 것이다.

 나. 가용속도장(可容速度場)

 가용속도장은 일반적으로 운동학적인 파괴메커니즘을 수학적으로 나타낸 것인데, 다음과 같은 2개 조건을 만족해야만 한다.

1) 변위의 경계조건으 만족한다.

2) 흐름의 적합식을 만족한다.

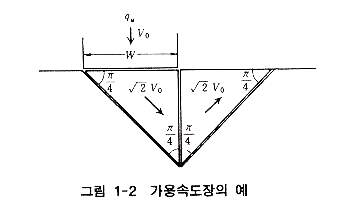
그림 1-2는 그림 1-1에 대한 가용속도의 한 예로서 기초저면이 활동하면 기초의 압입에 의한 외력은 그림에 2중선으로 나타낸 속도의 불연속선상에서 에너지가 소멸된다.

그림 1-2의 사용속도장은 45°의 2등변 3각형 2개 블록이 강체적인 활동 파괴메커니즘을 나타내고 있다. 조건 1)에 의하면 각 경계에 수직인 속도성분은 같아야 하며, 각 블록의 속도는 기초압입속도의  배로 해야 한다.

또한 조건 2)에 의하여 활동선상에서의 체적팽창은 0이다. 가용속도장에 으하면 외력과 내부소산을 같게 하여 지지력을 구하는데, 본 예의 경우 불연속선상에서 내부소산의 합계는 6 Cu W Vo, 외력은 qu W Vo 로 되면, 지지력은 qu = 6 Cu 로 구한다.

여기서, W는 기초폭, Vo는 가상기초의 압입속도이며, 정해치 5.14 Cu와 비교하면 가용속도장으로부터 상계값이 얻어지는 것이 알려져 이것을 증명한 것이 상계정리이다.

가용속도장은 가용응력장에 비하여 비교적 간단히 구할 수 있다. 복잡한 기하학적 조건에서도 실험에 의하여 비교적 합리적인 파괴메커니즘을 설정할 수 있는 경우가 많다.

이러한 의미에서 이용하기 쉬우나 설계에 직접 사용할 경우는 주의를 해야 한다. 그 이유는 가용속도장에서 구해지는 것은 상계값으로 위험측이 되기 때문이다.

따라서, 하계값이 구해지지 않는 문제에서는 실험에 의한 증명이 반드시 필요하다. 상계값이 계산결과가 어는 정도 정해값에 근접하는가는 오로지 가정한 파괴메커니즘, 다시 말하면 가용속도장이 어떻게 실제의 물리현상을 충실히 표현하는 가에 있다고 생각되기 때문이다.