14. 노상ㆍ노반의 변형계수(deformation modulus of subgrade and subbase)

 현재 아스팔트 포장은 CBR시험, 마샬시험 등의 결과를 이용하는 이른바 공학적, 경험적 설계법이 또한 콘크리트 포장에는 탄성상의 판 이론에 경험적 요소 및 온도 응력을 가미한 설계법이 각각 일반적으로 사용되고 있다. 그러나, 경험을 주로 한 공학적 방법에 의지하고 있는 것은 추론이나 응용이 가능하지 않고, 포장의 합리적 설계 또는 해석을 능률적으로 할 수 없기 때문이다. 그래서, 포장에 있어서도 다른 토목구조물과 같이 역학적인 설게 및 해석이 가능하듯이 많은 연구가 거듭되고 있다.

포장의 설계를 역학적으로 하는데 사용하는 이론체계에는 여러 종류가 있지만 그 중에서 대표적인 것은 탄성론일 것이다. 탄성론을 적용한 포장설계 이론은 많지만 현재에는 컴퓨터의 발달 보급에 으해 임의 의 복수원형등분포하중에 대한 다층탄성체 내의 응력, 변형 및 변위를 계산할 수 있게 되어 있다.

일반적으로 탄성론에는 물체의 변형특성을 나타내는 탄성계수 E, 포아슨비 υ를 사용하여 이론이 전개된다. 따라서, 탄성론을 포장 설게에 적용하기 위해서는 포장 각 재료의 E, υ를 알아야 한다.

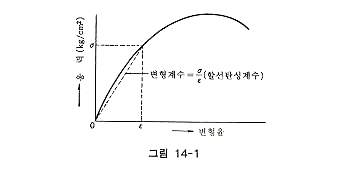
포장의 노상토 및 노상재료는 탄성체가 아니고 그 응력-변형곡선은 직선이 아니고 그림 14-1과 같이 곡선이므로, 모든 응력상태에 대하여 하나의 탄성게수로 표현하기가 불가능하여, 그림 14-1과 같이 할선탄성계수로 E를 고려하게 된다.

이와 같이 노상토나 노상재료의 E는 본래 완전탄성체의 탄성게수와 차이가 있기 때문에, 일반적으로 E를 변형계수라 부른다.

노상토나 노상재료의 변형계수를 구하는 데는 일축압축시험, 삼축압축시험, CVT시험방법, 평판재하시험 및 벤켈만빔시험에 의한 방법 등이 있다. 또, υ 탄성론에서는 그 값이 0 ∼ 0.5사이이고, 변형문제에서는 E가 다르더라도 큰 영향을 주지 않기 때문에 통상 0.5로 가정하는 경우가 많다. 삼축압축시험에 의하여 변형계수를 구하는 경우는 측압의 크기에 의해 그 값이 변화한다. 이 경우 현장의 노상토나 노상재료에 가해지는 실제의 측압을 고려하여 결정하는 것이 타당하다.

CVT시험은 직경 15cm, 높이 10cm의 시료를 직경 5cm의 플런지로 상하방향에서 압축하는 시험으로 변형계수는 플런저 변위량이 0.25cm 로 될 때의 하중강도를 0.025로 나눈 값으로 한다. 평판재하시험에 의한 방법은 포장을 각층 마다 다지면서 각층에서 시험으 하고, 완성된 포장에서는 포장표면부터 순차적으로 벗겨서 각층을 시험하고, 각층의 변형계수를 구한다. 벤켈만빔시험에 의한 방법은 포장을 각층마다 다지면서 각층에서 시험을 하고, 완성된 포장에서는 각층의 변위를 측정하기 위하여 소요심도까지 지름 10cm 의 코어보링을 하고 시험을 하여 각층의 변형계수를 구한다. 이 방법은 공용중인 포장재료의 변형계수를 계측하여 얻는 것이 특징이지만 계측치의 분포가 크기 때문에 많은 계측치를 요하고, 또 신속한 계측에는 상당한 숙련을 요한다. 또, 비파괴시험의 벤켈만빔을 개량한 다이나 플렉트가 개발되어 이것에 의한 포장역학의 조사연구가 이루어지고 있다. 다이나 플렉트는 포장에 진동을 주고 포장의 휨형상을 대단히 신속하게 구할 수 있는 기계로 앞으로 크게 이용되리라 생각된다.

표 14-1 노상ㆍ노반재료의 변형계수

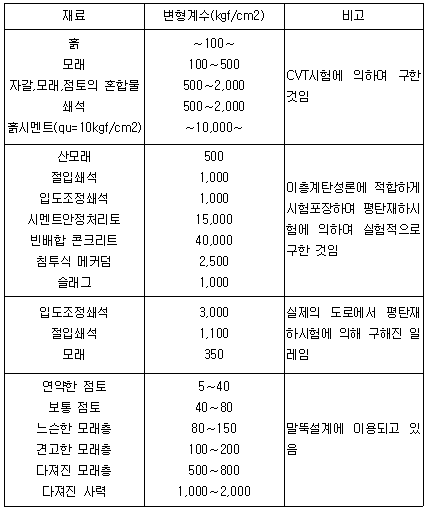
실측치로 구해진 노상토와 노상재료의 변형계수의 값은 표 14-1과 같다.

연약노상토의 아스팔트 포장공법인 샌드위치 포장에서는 이 설계를 적용한 적이 없고, 탄성이론이 적용된 예가 많다. 따라서, 이같은 포장의 추적조사를 하면 노상ㆍ노반의 적정한 변형계수를 구할 수 있다. 실제 포장의 각종 재료의 변형계수를 정확히 아는 것은 앞으로 포장설계 계산시의 가정을 더욱 실제적인 것으로 하기 때문에 중요한다.