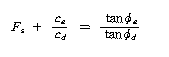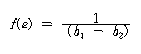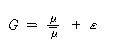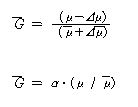54. 안전율(safety factor)

   가. 안전율의 역사

 기술분야에 있어서 "안전성"의 개념은 로마시대를 거슬러 올라간다. 단, 현재 사용되고 있는 정량적인 "안전율"의 정의는 아니다.

"안정성"을 정량적으로 설계에 사용할 의도로 "안전율"을 사용한 것은 중세 이후이다. Pugsley(1966)에 의하면 영국 Geoge 왕조(914-1830)시대 제분공장의 설계기사가 주철재의 기둥이나 보를 설계할 때 "안전율"을 사용하였다고 한다. 토질공학 분야에서는 아마도 Fellenius(1927)가 점착력 c, 마찰계수 tanφ를 사용하여 나타낸 식이 최초라고 생각된다.

윗 식에서 첨차 e, d는 각각 유효(effective), 동우너된(developed)의 의미를 나타낸다.

그런데 "안전율의 정의"가 논의의 대상이 된 것은 高岡에 의하면 1929년 경 000000의 논문이 최초이며. Pugsley(1939), Freudenthal A..M(1945)은 그 후의 연구라 할 수 있다. 이들 선구자는 어떻든 간에 구조설계분야에서 확률론을 도입하고 있다. 즉, "안전율"을 파괴확률과 관련시키도록 하는 방법을 시도했는데 토질공학분야에서는 Lazard(1961)가 최초로 생각된다.

   나. 안전율이 갖는 의미

 설계나 시공에서는 각종 요인으로 불확실성이나 불가피성이 개입된다. 이들을 크게 나누어 ① 모델오차 ② 불균일 ③ 불완전정보 ④ 개인오차의 4가지이다. 이들의 불확실성이 존재하기 때문에 기술자는 예기치 않은 파괴로 큰 손실을 여러번 경험하여 왔다. 이 같은 불확실성이 가져오는 손실을 위험(risk)이라 부르며, 인류의 역사는 당양한 위험에 대한 도전의 역사라 해도 관언은 아니다. 간단한 예제로서 포화된 연약점토지반 위에 성토를 급속히 시공하는 경우 φu = 0법에 의한 설계를 하면 원호 활동면을 가정한 φu = 0 법에는 앞서 기술한 모델오차 e가 포함되어 있다. 이 때 관용의 모멘트 비에 의한 안전율을 G라 하면 참의 안전율 F는 식(2)로 나타낼 수 있다.

e 값은 Bishop 과 Bjerrum 및 中賚의 실제 파괴예에 의해 검토한 결과 -0.1∼+0.1 범위의 분산성이 있다. 따라서 이를 일정한 랜덤(ramdom) 변수로 보고 그의 상하한치를 b1, b2라 하면 확률밀도함수 f(e)는 다음 식으로 주어진다.

한편 전단강도는 지반 내에서 위치적으로 랜덤에 분산성이 있으므로 저항모멘트와 활동모멘트의 비로 주어지는 관용의 안전율 G는 활동면에 따른 전단응력을 , 전단강도의 공간적 평균치를 μ라 하면 다음 식으로 표시된다.

단, ε은 전단강도의 분산성에 기인하는 G의 랜덤 변동성분이다. 식 (2),(4)에서 참의 안전율 F는

로 하면 식 (5)가 성립한다.

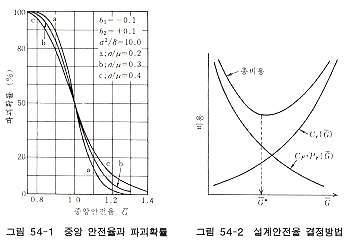
예를 들면 설계에서 bar G > 1.0 으로 되어 있어서도 e와 ε의 영향으로 우연히 F≤1.0으로 되는 경우가 있을 수 있다. 이같은 경우가 나타날 가능성을 파괴확률이라 부르며, 파괴확률과 bar G의 관계는 그림 54-1과 같은 형이 얻어진다.

그림에서 σ/μ는 지반 내 전단강도의 변동계수를 나타내며, σ2/δ는 활동면을 고정할 때 활동면에 연한 강도의 분산도를 나타내고 있다. bar G는 중앙안전율(central safety factor)이라 부르며 확정적인 관용의 안전율에 해당한다. 실제 설계에서는 e 나 ε의 영향을 생각하여 μ 대신에 μ-Δμ를 bar μ 대신에 bar μ-Δbar μ를 사용하여 식 (6) 또는 계수 α를 첨가하여 식(7)로 하여 결과적으로 F>1.0이 되도록 경험적인 G 값을 결정하고 있다.

식 (6),(7)을 사용한 관용의 안전율 G값의 결정방법은 완전히 경험에 의존하므로 합리적이 못된다는 비판도 있다. 그런데 그림 54-1과 같이 중앙안전율과 파괴확률의 관계를 이용하여 가장 합리적으로 안전율을 결정하도록 하는 방법이 長尾, 松尾, 黑田에 의해 제안되었다.

그림 54-2는 그 고려방법을 나타낸 것으로 중앙안전율 bar G를 크게 하면 건설비용이 크게 되는 반면 그림 54-1의 관계에서 기대되는 위험(Risk)은 저하한다는 관계가 있다. 따라서 전체비용을 최소화하는 bar G가 가장 합리적인 값으로 생각된다. 이 같은 안전율은 역사적으로 보아 상당히 다루는 방법이 변화되었으며 경험이 없는 구조물을 설계하는데는 이 같은 방법을 도입하게 되어 있다.