81. 인터록킹(interlocking)

 모래가 입자 집합체로서 나타내는 내부마찰각 Φ는 개개 입자 표면에 작용하는 입자간 마찰각 Φμ와는 물리적으로 다른 내용을 나타낸다.

φ는 같은 종류의 흙재료에 있어서도 입자배열, 밀도, 함수비, 시험조건 등에 따라서 다른 값을 나타내며 전단저항각이라 부르는 경우가 많다. φμ는 활동 및 회전 마찰을 포함하며, 같은 흙재료에 대하여는 그 상태나 시험조건에 관계치 않는 기본적인 재료정수이다.

φ와 φμ의 차이는 인터록킹(interlocking)에 기인하는 것으로 여기서 입자는 입형이나 파쇄가 생기지 않는다고 보고 같은 모래의 φ가 입자배열, 밀도, 함수비 인터록킹이 입자배열에 의존하기 때문이다.

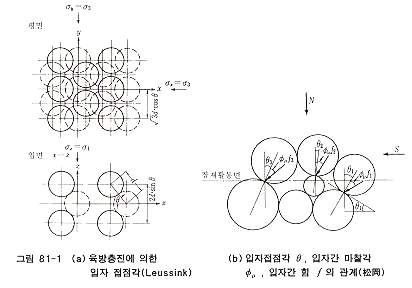
인터록킹은 개개 입자의 "맞물림"으로 번역되나, 입자가 간단히 맞물려 있는 것이 아니고 외력 특히 전단응력 작용 방향과 입자의 기하학적 구조와의 관계에서 정의되는 것이다. 일반적으로 인터록킹은 그림 81-1에 나타낸 입자접점각(또는 입자 접촉각) θ에 의해 표시된다.

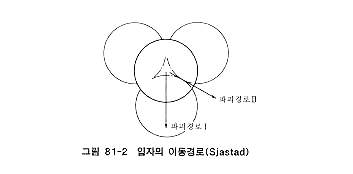
여기서, 입자접점각이란 그 입자의 접점에서 법선이 어는 기준 방향에 대하여 이루는 각이다. 같은 크기의 구의 집합체에서 간극비는 θ의 합수로 주어지며, 또 입자 이동 경로는 그림 81-2와 같이 2개의 경로, 즉 입자의 정점을 타고 넘는 경로와 입자의 계곡을 타고 넘는 경로가 있으며, 어느 경로를 취하는가에 따라 φ와 φμ의 관계가 다르다.

φ와 φμ의 관계는 구입자의 규칙적 배열에 관한 힘의 평형을 고려한다 든가 확률, 통계적 고찰을 한다든가 하여 많은 연구가 이루어지고 있다. Caquot는 다양한 크기와 형태의 입자로 된 임의 입자배열의 모래에 대하여 확률, 통계적 고찰을 하여 평면 변형상태에서 φ와 φμ의 관계를, 또 Bishop 은 모래의 실험적 고찰에서 삼축압축 및 평면변형 상태에 대하여 φ와 φμ의 근사적 관계식을 얻었다.

Farouki 와 Winterkorn은 구입자가 규칙적으로 배열되어 있는 입상체의 φ와 φμ의 관계에 대하여 많은 연구를 소개하고 있다.

더욱이 모래의 변형 메커니즘의 미시적 고찰에서 Newland와 Alley, Rowe, 小田, 松岡 등은 모래의 강도 변형관계식에 φμ 및 입자접점각을 고려하고, 落合은 직접전단 메커니즘의 고찰에서 φ와 φμ 의 관계를 유도하고 있다.

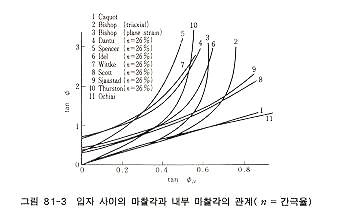
대표적인 φ와 φμ 의 관계는 그림 81-3에 나타냈으며, 이 그림에서 Caquot, Bishop, Thurston 및 落合의 관계곡선은 원래 원점을 통과하는 것으로 그들의 φ는 체적을 일정하게 하여 전단시킬 때 즉, 임계 간극 상태에서 φcv를 표시하며, 다른 곡선은 φμ = 0 에서도 φ>0 이 된다.

Reynolds는 1855년 나온 입상체 거동을 특징짓는 다이레이턴시는 인터록킹에 기인하는 것으로서 전단강도에 미치는 인터록킹의 기여를 인터록킹 효과라 부르고 있다. 견고하게 맞물려 있는 일정한 체적의 모래가 전단을 받을 때 입자 이동은 인터록킹에 의해 방해를 받으므로 입자간 내부마찰이 완전히 작용하기 위해서는 먼저 입자배열이 느슨하게 될 필요가 있다. 이에 따라 생기는 체적 팽창이 정(+)의 다이레이턴시라 하고, 느슨한 상태의 모래는 인터록킹에 의해 아치(arch)구조를 갖고 있다고 생각되며, 전단에 의해 그의 아치가 파괴되어 입자배열이 변하는 과정에서 체적수축이 생기는데 이를 부(-)의 다이레이턴시라 한다.

인터록킹은 모래의 내부적 일에 관계되며, 다이레이컨시에 의한 표면에너지 보정은 모래의 외부적 일에 관계한다.

조밀한 모래에서 인터록킹이 내부압(intrinsic pressure)이라 하여 효과를 갖는 경우 그 모래는 인터록킹에 기인하는 겉보기 점착력을 갖는다.