95. 지오스태티스틱스(geostatistics)

 이것은 지구통계법, 지질통계법 또는 지반통계법 등으로 불리고 있는데 넓은 의미로서는 예를 들면 암반중 균열 주향경사의 슈미트네트(schmidtnet)에 의한 해석 등, 지질, 지리에 관한 통계가 포함되며, 일반적으로는 좁은 의미로서 바리오그램, 그리킹을 사용하는 공간적 통계방법을 토대로 하는 일종의 보간법이라 할 수 있다.

종래 표본(sample)지점 사이의 보간법으로서 표본지점 사이의 차이를 이용한 거리반비례법, 거리차 2제곱의 반비례법 또는 표본지점간 2등분선을 그려서 구하는 다각형법 등이 이용되어 왔으나 이들의 방법은 간단히 기하학적으로 추정하는데 불과하므로 신뢰도가 높은 추정을 하기 위한 한 방법으로서 지오스태티스틱스가 제안되었다.

이를 토대로 하는 추정법은 크게 2단계로 나누어 진다. 여기서 1단계는 바리오그램에 의한 대상 공간의 구조해석이며, 대상 공간 고유의 함수를 구할 수 있다.

지오스태티스틱스는 어느 영역 내, 예를 들면 지질구조적으로 같다고 생각되는 영역 내에 있으면 표본치의 분포는 같으며, 표본의 간격과 배열만 관계되는 것으로 가정한다.

이 시료 무리의 간격과 배열에 의한 관계를 표본치 차의 분산으로 표현하며, 이 분산을 바이오그램이라 한다. 그림 95-1은 바리오그램을 계산하기 위한 표본의 예로서 측선을 따라 평행할 경우 먼저 단거리 1d 만큼 떨어진 모든 표본 폐어(pea)를 구하고 바리오그램을 계산한다.

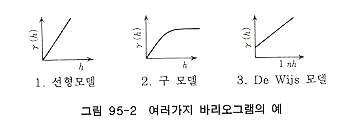
같은 방법으로 2d, 3d,..., nd와 각 표본 페어에 대하여 바리오그램치를 계산하고 이것을 그림 95-2와 같이 거리-바리오그램 관계도를 작성한다. 이렇게 얻어진 세미바리오그램 곡선으로부터 이 공간의 특성을 고려한 고유의 이론 바리오그램을 구한다.

이론 바리오그램은 몇 가지가 있는데 그 대표적인 것이 그림 95-3이다. 이중 자연계의 현상, 특히 지질현상에 관해서는 구모델이 많이 알려져 있다.

제2단계는 이 바리오그램 함수를 바탕으로 그리킹을 사용하여 최적의 무게를 계산하고 계산 대상 블록의 값을 추정한다. 동시에 추정 값의 정밀도를 계산한다.

어는 점의 값을 추정할 경우 근접하는 영역의 표본치에 적당한 무게를 예측하며, 지오스태티스틱스에서는 그 무게를 추정하는 영역을 포함, 대상공간 고유의 함수인 바리오그램으로 구한다.

이대 그 추정오차의 분포가 최소로 되도록 무게를 계산하는데 이 무게를 계산하는 방법을 그리킹이라 한다.

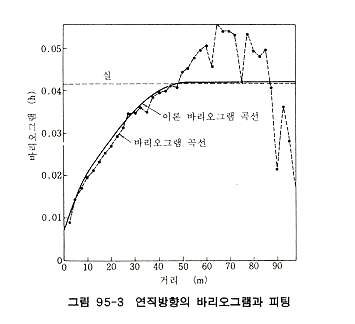
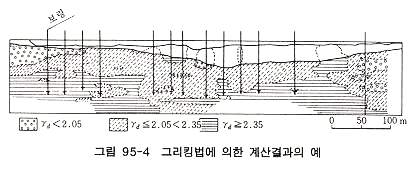
보링 코어의 건조밀도 측정결과를 토대로 보링공 사이의 밀도분포를 추정한 예를 들면 그림 95-4와 같이 어느 지점에서 30∼120m 간격으로 연직 보링을 하고 채취한 코어는 0.5m 간격으로 건조밀도가 측정되어있다.

계산 영역은 대부분 지질구조를 지배하고 있다고 생각되는 단층에 끼여있는 영역으로서 계산 정밀도를 높이기 위하여 동일 단면상의 보링뿐만 아니라 전후의 보링결과도 고려하였다.

1개 추정 블록의 크기는 보링간격, 밀도측정 간격 등을 고려하여 2.5X10X10m로 하였다. 그림 95-2는 연직방향의 바리오그램곡선으로서 약 50m를 넘으면 바리오그램 값은 변화가 많아 여기까지를 영향범위로 하여 구모델을 적용하였다.

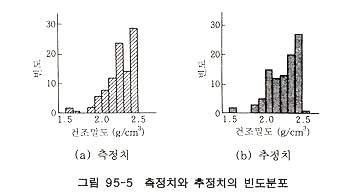
수평방향 바리오그램은 연직방향과 같은 바리오그램을 사용하며, 양방향의 기하학적 이방성을 고려하여 범위의 비율을 변경하였으며 그림 95-4는 그 추정 예이다. 이 장소에서는 연직 및 수평보링이 실시되어 있어 그 결과를 사용하여 검증한 것이 그림 95-5이다.

측정치와 추정치는 잘 대응을 하고 있어 전체로 보아 추정에 별 문제가 없음을 알 수 있다. 단 각각의 점을 비교하면 양자의 상관성이 낮은데 그 이유는 추정 블록 형상이 영향을 주고 있다고 생각된다.

지오스태티스틱스는 보간을 위한 통계방법이므로 지질, 토질조사에서 N 치, 밀도, 투수계수, 일축압축강도, 변질정도, 루존값 등 분포의 추정, 강우량 분포 추정 등 어느 규약적 변화를 나타내는 현상에 적용이 가능하다고 생각된다.

특히 이 계산법에서는 추정치의 오차분포 분산도 알 수 있으므로 조사부족 장소의 발견 및 다음 단계 조사장소의 선정에도 효과적이며, 어느 현상을 추정할 경우 1종류의 측정치에 의한 추정뿐만 아니라 복수의 측정치를 사용하여 추정하는 방법도 있어 앞으로의 응용발전이 기대된다.