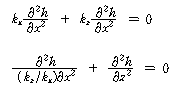101. 침투류(seepage flow) |
|
||
|
|
|
|
|
|
|
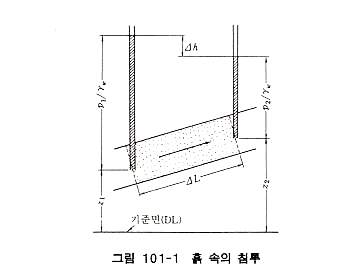
지구 표면을 덮고 있는 흙은 골조를 형성하는 고체성분인 흙입자와 그 간극을 채우고 있는 물 또는 기체(공기)로 구성되어 있다. 그리고 흙 중의 물은 일반적으로 크게 나누어 지하수위 하에 있는 포화대와 그 상부의 비포화대로 분류되며, 후자는 모관수대와 피막수대 등으로 분류된다. 일반적으로 흙입자 간극내를 물이 이동하는 상태를 투수 또는 침투라 하며, 그 흐름을 침투류라고 한다. 그러나 비포화대의 침투와 포화대의 침투는 그 형태가 다르다. 즉, 전자는 지표면에서 빗물의 침투와 같은 불연속적인 흐름이며, 후자는 지하수와 같은 연속적인 흐름이다. 보통 토중수의 침투는 후자의 연속적인 흐름을 가르키며, 비포화대의 불연속적인 흐름은 이와 구별하는 의미에서 비포화 흐름이라 한다. 포화수대와 모관수대의 경계면은 대기압과 접해 있으므로 일반적으로 자유수면 또는 지하수면이라 부르며, 하천제방, 필댐 등에서는 침윤선이라 한다. 지중의 침투는 전수두의 차이에 의하여 생기며, 전수두가 높은 곳에서 낮은 곳으로 물이 흐르며, 어느 점의 전수두 h는 그림 101-1과 같이 위치수두와 압력수두의 합계로 정의된다.
한편 위치수두는 임의로 정한 기준면에서의 연직거리 Z, 압력수두는 이 점의 간극수압(pw)을 물의 단위중량(γw)으로 나눈 수주높이 (pw/γw)이다. 그림 101-1에서 ΔA, 길이 ΔL의 미소 요소를 고려하여 이 사이의 수두차를 Δh로 하면 이 방향의 단위시간당 유량 Δq는 다음 식으로 구할 수 있다.
윗 식은 1856년 Darcy가 제안한 것으로서 Darcy 법칙이라 하며, 유속은 Vs = Δq / ΔA 로 되는데 이것은 겉보기유속(배수속도)으로서 흙의 간극을 통과하는 실제의 유속은 아니다. 실제유속(vs')은 Δq를 ΔA 내의 순간극면적으로 나눈 것이므로 간극율(n)을 소수로 나타내면 (간극면적 nΔA), vs' = ki/n = vs/n 으로 된다. 이것은 토중 침투현상을 1차원적으로 취급한 것이며, 대부분의 경우 이러한 문제는 2차원적으로 취급된다. 토중의 미소 요소를 통과하는 수평방향(x), 연직방향(z)의 속도성분을 각각 Vx, Vy 로 하면 침투류의 연속식은 다음과 같다.
여기서, vx 와 vy 는 식(1)에 의하여 다음 식으로 구할 수 있다.
식 (2)에서 φ = kh 로 하면 식(4)의 Laplace 방정식이 구해진다.
여기서, φ는 속도수두라 부르며, Darcy 법칙은 지중의 모든 침투문제에 적용되는 것은 아니며 유속이 크면 성립되지 않는다. 그 한계는 손실수두(Δh)와 유량(Δq) 사이의 선형관계를 잃고 흐름이 층류에서 난류로 이행하는 유속이다. 유선망의 경계조건이 비교적 간단한 1차원 문제에서는 식(1)을 그대로 사용하여 침투유량을 구할 수 있으나 일반적으로는 식 (4)를 적당한 경계조건을 가지고 푸는데 해석방법으로 최근 가장 많이 사용되고 있는 것은 유한요소법이며, 유한차분법 등도 사용되고 있다. 유선망을 그리면 침투유량, 임의의 간극수압(양압력)의 크기를 알 수있고 이로서 유효응력의 평가, 흙구조물의 안정성 검토를 할 수 있다. 식(4)의 풀이는 모든 점에서 직교하는 2개의 곡선군으로 표시되는데 그 하나는 유선, 다른 하나는 등수두선이 된다. 이 두 곡선은 침투영역에서 망눈과 같이 많이 그릴 수 있으므로 이를 유선망이라 하며, 실제는 이것은 서로 직교하는 유선과 등수두선 무리로 경계를 가지는 사각형으로 이루어지며, 그림 101-2와 같이 거의 정방형에 가깝게 되도록 수정을 반복하여 그린다.
유선이 그림 101-2와 같이 그려질 경우 단위길이당 침투유량 Q는 다음 식으로 구할 수 있다.
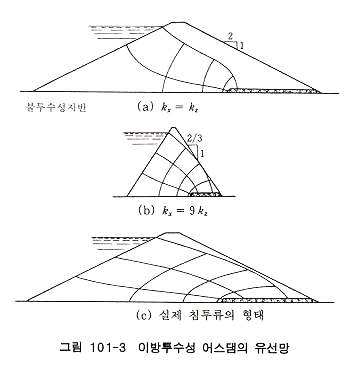
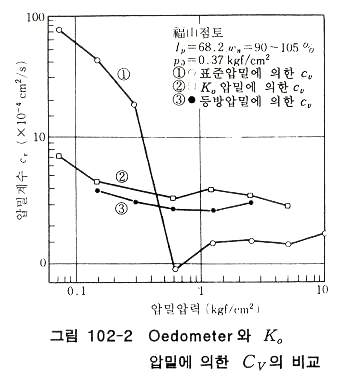
유선망이 있어서 1개의 망눈의 손실수두는 Δhdlamfh 그림 102-2의 p점이 상류면(전수두 H2)에서 np 째 망눈에 해당하는 것으로 하면 그 점의 전수두 Hp 는 Hp = H2 - np(H2-H1) / Np 로 된다. 따라서 Hp에서 이 점의 위치수두 Zp를 빼서 압력수두를 구하며, 여기에 물의 단위중량을 곱하면 간극수압을 구할 수 있다. 침투계수의 이방성에 있어서 식 (3)의 우변은 침투중 흙의 용적변화가 생기지 않는다고 보고 구한 것이므로 식(6)이 성립된다.
여기서 (kz / kx) 1/2 ㆍx = xi 로 하면 식 (7)은 kx = kz 의 경우 식(4)와 같게된다. 이것은 kx ≠ kz 의 경우 유선 또는 선망 작도에 있어 x 축 방향을 (kz / kx)1/2 만큼 축척해야 한다는 것을 의미하는 것이다.
예를 들면 그림 101-3(a)는 kx = kz의 유선망, (b)는 kx = q kz , 즉 수평방향(x)를 (kz/kx)1/2 만큼 축소하여 유선망을 그린 것이며 또한 (c)는 (b)를 원래의 형상으로 복귀시킨 것인데 실제의 침투류는 이 형태로 된다. |
|
|
|
|
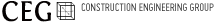

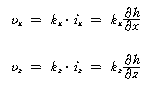 (3)
(3)
 (5)
(5)