
103. K 치(K value) |
|
||
|
|
|
|
|
|
|
공학적으로 자연현상을 해석하기 위해서는 가능한 자연현상을 충실히 표현하는 해석모델을 설정해야 한다. 해석모델에 따라서 수학적인 방정식을 세우고 이를 해석함에 따라 자연현상의 모의조작(simulation)을 시도한다. 예를 들면 그림 103-1에 나타낸 것은 1질점 1자유도계의 진동모델로 진동현상을 해석하기 위한 가장 간단한 모델로 상당히 넓은 분야에 이용되고 있다. 이 모델에서 m은 질량, K는 탄성계수, c는 감쇄계수이며, K 치로 표현되는 탄성계수는 kgf/cm2 의 단위를 갖는 복원력이다. 복원력의 물리적 의미를 더욱 쉬운 말로 표현하면 물체에 힘을 가하면 물체는 변형하고 원래대로 돌아오려고 하는 힘이 내부에 에너지로서 축적된다.
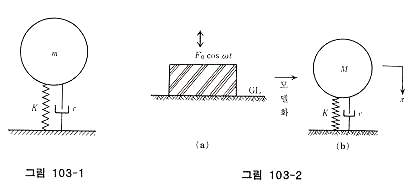
이와같이 원래대로 돌아오려고 하는 힘을 복원력이라 부르며, 탄성게수 즉 복원력은 힘을 가한 물질의 응력-변형곡선의 접선기울기이다. 그림 103-1에 나타낸 모델에서 탄성계수 K를 구성하는 물질이 금속 또는 다른 탄성체로 되면 그 재료가 항복할 때 까지 일정치를 갖는다. 그런데 지반은 탄성체가 아니며, 변형이 작은 범위에서는 탄성체와 유사한 거동을 나타낸다. 지반과 구조물 등 상호작용을 해석할 때 이같이 질량이 없는 탄성으로지반을 표현할 수 있으면 다양한 해석모델이 아주 간단한 형으로 표현된다. 토질기초공학 분야에서는 지반을 질량이 없는 탄성체로 치환하고 그 탄성계수를 K 치로 부르고 있다. 그 말은 다른 공학에서 탄성게수를 K로 표현하는 경우가 많기 때문에 이에 준한 것이다. 지반과 구조물의 상호작용이 상당히 중요한 연구과제로 되어 요즘은 K 치는 내진공학에도 자주 사용되고 있다. 또 Kcl의 단위면적당 값을 k 치로 표시하여 kgf/cm3 으로 나타내는 경우도 많다. 여기서 주의하여야 할 것은 지진학에도 K 치라는 말이 지금까지 기술한 것과 아주 별도의 의미로 사용되고 있는 것이다. K 치라는 전문용어가 잘 사용하는 것은 토질공학, 토목공학, 토질기초공학, 건설공학, 내진공학 등의 분야에 한정되는 것에 주의하기 바란다. 이 K 치의 이용 예는 그림 103-2(a)와 같이 기계기초의 설계를 할 때 통상 그림 103-2(b)와 같은 모델로 진동해석을 하는 것이 일반적이다. 이와 같은 의미로 구조물과 지반의 상호작용을 고려할 때 같은 모델을 고려할 수 있다. 그림 103-2(b)의 진동해석 모델의 방정식은 다음 식 (1)로 된다.
이를 풀어서 외력의 원진동수 ω와 계의 고유원 진동수가 일치하지 않도록 한것이방진설계의 기본이다. 이들의 K 치는 지반과 기초의 접촉면만 아니라 지하구조물(케이슨, 지하벽 등)의 수평복원력을 나타내는 지수로서도 사용되고 있다. 그림 103-3(a)에 나타낸 지반위에 놓인 보의 강도해석에는 탄성슬래브 위의 보이론이라 하는 해석방법이 잘 이용된다. 그림 103-3(b)에 나타낸 말뚝의 횡저항을 해석하는 모델도 종종 이 방법이 사용된다. 이들의 해석을 위한 기초방정식은 보의 췸강성을 EI라 하면 다음 식(2)으로 나타낼 수 있다.
또 이들의 방정식에 고나성력(pA)의 항을 도입하면 진동방정식(2)가 된다.
이와같이 K 치의 응용범위는 상당히 넓고, K 치를 사용한 해석ㄹ모델도 아주 간단하게 되며 그의 해를 구하는 것도 비교적 간단하다. 그러나 K 치는 지반의 물리정수와 그와 상호작용을 갖는 기초구조물의 형상과 관련되기 때문에 이를 구하는 것은 간단한 것만이 아니다. 많은 실험자료를 수집하는 것이 중요하고 이를 구하기 위하여 복잡한 이론해석이 필요한 경우도 있으며, 특히 요즘 내진공학분야에서 이 값을 구하는 연구가 중요한 초점이 되고 있다. |
|
|
|
|
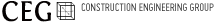
 (2)
(2)