115. 한계해석(limit analysis)

 지반이 어느 지정된 조건을 가지고 소성변형을 할 경우 흙의 항복조건, 흐름의 적합성, 힘의 평형식, 힘 및 변위의 경계조건 등 모두를 만족시키는 응력, 변위를 정하기는 일반적으로 어렵다.

고로 조건을 완화하여 일부 조건만을 만족시키는 근사해라고 하는 편법이 고려되고 있다. 흙을 완전강소성체라는 개념을 가지고 상기 조건 중 다음 3조건을 만족시키는 응력계를 가용응력장이라 한다.

① 모든 부분에서 항복조건을 만족시킨다.

② 응력의 평형조건을 만족시킨다.

③ 경계응력의 경계조건을 만족시킨다.

이때 경계응력치는 정해를 초월하는 것이 아니고 지지력 문제 등 광의의 수동토압 사이의 문제에서는 하계치가 주어지는데 이를 하계정리라 한다.

④ 변위의 경계조건을 만족시킨다.

⑤ 흐름의 적합성을 만족시킨다.

상기의 2개 조건을 만족시키는 속도계를 가용속도장이라 하며, 이 때 속도의 불연속 상에서 소산되는 내부소산과 외력을 등치로 구하는 경계응력은 정해에 뒤지지 않는 상계치가 주어지는데 이를 상계정리라 한다.

이들의 증명은 흙의 재료특성이 항복함수와 소성포텐셜이 일치하고 또한 항복곡면이 요철형이라는 조건과 함께 최대소성일의 원리, 가상일의 원리로부터 도입된다.

즉, 한계해석은 상계정리, 하계정리를 이용하여 정해치를 구하는 해석법이라 할 수 있으며, 일반적으로 가용속도장은 가용응력장 보다 직관적으로 보기 쉽다.

파괴형식은 실험에 의해서도 파악할 수 있으며, 이 파괴형식에 몇 개의 형태를 도입하여 각각에 대한 변분을 취하여 극소의 상계치를 계산할 수 있다.

이 극소 상계치에 의하여 비교적 정해에 가까운 결과를 얻을 수 있으며, 이와 같이 하계를 구하지 않고 상계만으로 해를 얻도록 하는 방법이 많이 이용된다.

일반적으로 하계를 구하기는 어려우며, 상계정리 이용 순서를 대상기초의 지지력 계산에 대하여 기술하면 다음과 같다.

  가. 파괴형식의 결정

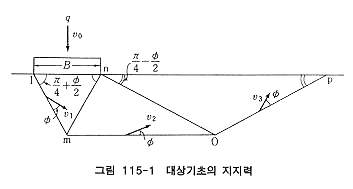
 운동학적으로 무리없는 파괴형식을 가정하여 그림 115-1의 예와 같이 몇 개의 강체블록으로 나누어 파괴형식을 고려한다.

  나. 흐름의 적합성 조건 부여

 이 조건은 운동하는 강체블록의 속도가 정지역에 대한 φ 만큼의 경사를 가지게 한다.

  다. 속도경계역 부여

 강체블록은 속도의 경계조건을 만족시키므로 각 강체블록의 연직속도 성분이 같은 조건으로 주어지며, 각 블록의 속도 및 각 블록의 경계선을 따라 속도의 불연속량이 경계속도(vo)로 나타난다.

예를 들면 속도(v)는 vo = v1 sin(π/4 - φ/2), v1 = v2 sin(π/4 - φ/2) 등이 성립되고 속도의 불연속량 (δv)은 그림 116-1의 lm에 연하여 δvlm = v1 cos φ, mn에 연하여 δvmn = v2 cos(π/4 - φ/2) 등이 구해진다.

  라. 내부소산과 외력일 등치

 단위면적당 내부소산은 속도의 불연속량(δv)에 점착력(c)을 곱한 것이므로 전 내부소산은 모두 불연속선 위에서 소산을 합한 것이다. 전외력일은 경계응력과 중력에 의한 것의 합계로서 양자를 등치로서 미지량의 경계응력을 구한다.

이상과 같이 그림 115-1에서 가정한 파괴형식에 대한 미지량 q를 구할 수 있으나 전술한 여러 가지의 파괴형식 중에서 최소지지력을 가지는 형식을 해로 한다.