42 소성유동 (plastic flow)

 물질 변형의 기본적인 형은 가역적인 탄성변형과 비가역적인 유동이 있다. 여기서 유동은 점성유동과 소성유동으로 나누어 지며, 일반적인 레올로지에 있어서 소성유동의 정의와 토질공학에서의 정의가 다르다.

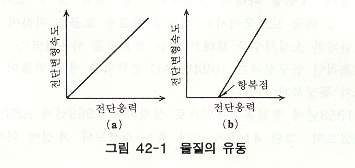
항복치는 물체 내의 일부 또는 전부에 비탄성변형이 생기기 시작할 때의 응력을 말한다. 이상적닌 점성유체로서는 그림 42-1(a)와 같이 항복치는 0이므로 무한소의 전단응력이 작용하여도 점성유동이 생긴다.

따라서 이러한 액체는 정수압 이외의 압력을 정지상태에서는 지지할 수 없다.

그런데 어는 물질에서는 물질 내의 전단응력이 항복치를 넘으면 그림 42-1(b)와 같이 점성유동이 생긴다.

일반적인 레올로지에 관한 교과서에서는 이러한 유동을 소성유동 또는 Bingham Flow이라 한다.

한편 토질공학에서는 소성유동이란 말을 전술한 항복치를 넘는 점성유동이라는 의미로 사용되는 것이 아니라 소성변형의 의미로 특히 지반의 소성평형과 관련하여 사용되고 있다.

소성변형은 점성유동과 같이 비가역적인 변형의 하나인데 시간요소와 전혀 관계가 없는 점에서 점성유동과 구별할 수 있다.

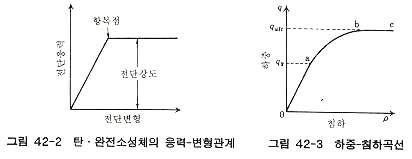
그림 42-2와 같은 응력-변형특성(탄ㆍ완전소성)을 나타내는 등방등질지반 위에 대상기초를 설치할 경우 대상기초 단위면적당 하중강도가 증가함과 함께 대상기초에 접하는 지표면은 침하한다.

이 침하량과 하중강도 q(=P/A)의 관계는 일반적으로 그림 42-3에 나타낸 곡선 oabc 와 같다. 여기서 P는 전하중, A는 기초의 저면적이다. 하중강도가 항복치 qy (Py/A)를 넘지 않는 구간은 지반내 모든 흙요소가 탄성적으로 나타나며, 그림 43-3의 oa와 같은 직선관계가 얻어진다.

하중강도 qy를 넘으면 지반내 어는 영역에서는 흙요소가 항복하기 시작한다. 더욱이 하중강도가 증가함에 따라 소성역이 확대되고 침하가 급증한다. 그래서 하중강도가 극한지지력 qult 에 도달하면 지반내에서는 연속적인 활동선이 형성되어 지반은 파괴상태(직선 bc의 상태)에 이른다.

하중강도 qy에서 qylt 에 이르는 구간(곡선 ab)에서 지반은 소성역의 확대를 수반하면서 변형하는데 이 지반의 변형형식은 D'Appolonia 등은 국부 소성유동(contained plastic flow)이라 하고 있다.

이러한 소성유동 성상을 더욱 구체적으로 파악하기 위해서는 다음 사항을 검토해야 한다.

① 항복하중과 흙의 전단강도 관계

② 소성역의 확대성상

③ 최초로 항복되는 흙요소의 위치

④ 극한지지력과 흙전단강도의 관계

⑤ 파괴시의 소성역

이들 항목에서 비교적 간단히 알 수 있는 것은 φ=0° 인 재료에 대한 것이며, 앞으로의 설명은 이 재료에 대한 것이다. 지금 대상토가 Tresca의 항복규준에 따라 항복한 그림 42-2의 탄ㆍ완전소성체로 본다.

그리고 흙의 비배수전단강도 cu를 주응력차의 1/2이라고 정의하면 Tresca의 항복규준은 다음과 같다.

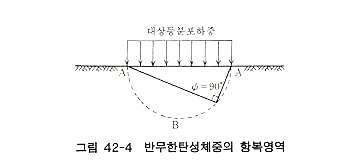
한편 그림 42-4와 같은 등분포 대상하중을 받는 반무한 탄성지반내의 응력분포는 해석적으로 구해지며, τmax 는 다음과 같은 관계가 있다.

상기 식에서 τmax 값은 φ=90도 일 때 최대로 되며, 그림 42-4와 같이 재하폭 AA를 지름으로 하는 반원 ABA위에서 흙요소는 최초로 항복됨을 알 수 있으며, 항복하중 qy 는 다음 식으로 구할 수 있다.

하목 ④, ⑤에 대해서는 종래부터 흙을 강소성체로 이상화하여 활동선장의 이론을 적용하여 결과를 얻은 것인데 φ = 0 인 재료의 표면에 설치된 대상기초의 극한지지력 qult 는 다음 식으로 구할 수 있다.

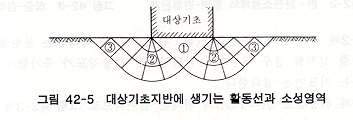
지반이 극한(파괴) 상태일 경우 Prantl 은 소성영역을 그림 42-5의 영역 ②, ③을 고려한다. 또한 그림 중의 ①영역은 대상기초와 일체로 되어 침하 하는 강성영역이다.

항목 ③에 대해서는 상기와 같은 탄성응력이론 및 활동선장의 이론은 적용할 수 없으며, 이 문제에 대해서 최초로 좋은 성과를 얻은 것은 H eg 등이다.

이들은 Tresca의 항복기준에 따라 탄ㆍ완전소성체 위에 대상하중을 가할 경우의 지반거동을 럼프크 파라미터 모델(lumped parameter model)의 방법으로 해석하고 극한지지력은  식(4)으로 정확히 예측할 수 있으나 소성영역 성장의 양상은 고전이론으로 예상되는 것과는 상당한 정도로 차이를 나타내고 있다.

즉, H eg 등이 구한 결과에 의하면 최초의 항복은 그림 42-4중의 점 B 근처에서 생기며, 재하중강도의 증가와 동시에 소성역은 확대되어 극한상태에서는 그림 42-5의 역역 ②, ③ 아래쪽에 까지 발달한다.

단, H eg 등이 채용한 지반모델은 반무한체가 아니고 강한 기반상의 유한 두께의 지반이라는 것을 알아야 한다.

지반의 소성유동을 고려하여 설계, 시공지침을 작성할 경우에 참고가 된다고 생각되는 접근방식 2가지를 소개하면 다음과 같다.

점토지반 위의 구조물에 대한 전즉시침하량(Si)은 일반적으로 탄성론적인 방법을 이용하여 구하고 있으며, 이 때 지반의 소성유동에 대한 것은 무시한다. 그런데 D'Appolonia 등은 대상기초에 대하여 유한요소해석을 하고 지반의 소성유동을 고려한 구조물의 즉시침하추정법을 제안하였다.

즉, 그는 유한요소해석 결과를 3개의 무차원량 Se/Si, q/qult, f 사이의 관게를 도표로 만들었다. 여기서 Se/Si는 전즉시침하량(Si)는 점유하는 탄성침하량(Se)의 비율, q/qult는 극한지지력에 대한 하중강도의 비, f는 지반내의 초기응력상태를 나타내는 인자로서 다음 식으로 나타낼 수 있다.

일반적인 문제는 q/qult의 값(안전율의 역수)과 f값은 이미 알고 있으므로 작성한 도표에서 Se/Si를 구할 수 있다. 한편 탄성론에 의하면 Se의 값을 별도로 계산할 수 있으므로 이들 결과를 조합하면 전즉시침하량(Si)을 구할 수 있다.

또한 지반의 소성유동은 구조물기초의 침하성상에 연관될 뿐만 아니라 구조물기초 주변지반의 측방변위성상에도 연관된다. 특히 설계안전율이 비교적 적은 성토 기초지반의 경우는 지반파괴에 이르는 과정으로서 성토비탈 끝 부근의 측방변위와 그 속도의 발달과정을 파악하는 것이 지반파괴를 예측하는데 유력한 수단이다.