36. 삼차원 압밀(three-dimensional consolidation)

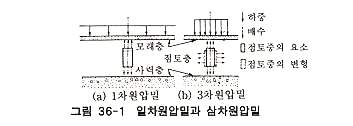
 압밀은 Terzaghi 의 압밀이론을 기본으로 하고 이는데, Terzaghi 의 이론은 가정에서 보통 압밀시험시의 시료 상태와 같은 조건으로 하고 있다. 즉, 시료의 측면은 구속되어 측방 변화를 허용하지 않고 압축은 연직축방향만이 생긴다. 또 시료내부의 물도 그 축방향으로 만 흐르는 것을 허용하고 측면 방향으로는 구속되어 있는 1차원 압밀이다. 이것은 매립지와 같이 점토층 두께에 비하여 폭이 넓은 데에 동일 하중이 걸린 경우를 가정한 침하해석이론으로 수십 m의 점토층 두께에 대하여 상부구조물의 폭이 수십 m 인 경우에는 적용되지 않는다. 이같은 경우에 점토층은 연직으로 압축될 뿐만 아니라 측방으로도 압출되어 변형하기 때문에 구조물의 침하도 일차원의 조건 보다도 더 많이 발생한다. 또, 재하에 의하여 구조물 직하의 점토층 중에 발생하는 과잉간극수압 때문에 점토층 중의 물이 연직방향뿐만 아니라 구조물 주위의 하중을 받지 아니한 부분의 방향으로도 흘러가게 된다. 이 같은 상태에서 점토층의 압밀은 삼차원적 압축과 삼차원적 간극수 흐름에 의해 발생하게 되는데 일반적으로 삼차원 압밀이라고 부른다.(그림 36-1 참조)

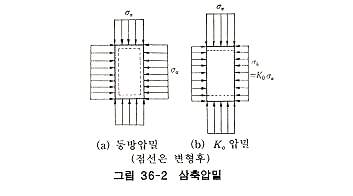
점토의 전단강도 정수 중에 압밀 비배수시험에 의한 값 Ccu, φcu 는 지반개량공법 설계시에 사용하는 강도 증가율 Cu/p 와 직접적으로 관계가 있기 때문에 중요한 정수이다. 이것을 구하기 위하여 삼축압축시험기 안에서 시료 주위에 페이퍼드레인을 설치하여 압밀한다. 압축하중은 보통, 액체압으로는 등방적으로 재하하지만 때로는 측압을 가감하여 시료의 직경이 변화하지 않도록 연직축방향에 만이 압축시험을 하는 경우도 있다 전자를 삼축등방압밀,후자를 Ko 압밀이라 부르는데 모두 삼축방향압축과 삼축방향배수에 의한 삼차원압밀의 예이다. 그러나  처음에 기술한 예와는 응력의 분산효과가 없는 등 다소의 성격이 다르기 때문에 삼축압밀(triaxial consolidation)과 구별하여 부르고 있는 경우가 많다(그림 36-2 참조)

삼차원적인 압밀침하량을 구하는 방법은 아직 확립되어져 있지 않고, 여러 가지 제안이 있으며, 다음과 같이 측방변에 의한 초기침하 또는 즉시침하와 그 후의 압밀침하로 나누어 별도로 계산하여 더하는 경우가 많다.

Si를 구하는 방법으로는 지반을 탄성체로 보고 비배수 조건(즉, 포아슨비 υ = 0.5)재하에 따른 전단변형을 이론적으로 계산하여 구하는 방법(Skempton)과 삼축비 배수시험의 변형량으로부터 구하는 방법(Lambe)으로 대별된다. 또, Sc를 구한느 방법은 반무한 탄성체 표면재하에 의한 응력의 분산효과를 고려하여, 지반중의 평균수직압밀응력을 구하고 그것으로부터 얻어진 일차원압밀침하량 So에 삼차원적응력에 의한 수정계수 μ을 곱하여 계산하는 방법이 더 많이 사용되고 있다. (Skempton). 그러나 μ의 값은 점토층 두께와 재하폭의 비 D/B 및 간극압계수 A의 함수이다.

그 외에 삼차원탄성이론에 의한 압축침하량 식중에 탄성계수 E, υ 등에 압밀종료시의 값으로 이론계산하는 방법도 사용되고 있다. 어느 경우도 이러한 방법에서는 탄성정수 결정방법이 문제가 된다. 또 근본적으로는 Si 와 Sc를 나누어 Si에서는 체적변화는 일으키지 않고 측방변형에 의해서만 침하가 생기는 경우이며 다이레이턴시 때문에 전단변형에 따른 압밀이 생기는 것은 아니므로 읷을 무시하는 경우에 의문이 있게 된다. 일반적으로 연약지반상 구조물의 하중강도가 극한지지력에 가깝게 되면 점토층은 측방유동을 일으켜 파괴침하적으로 점토지반중에 구조물이 깊이 빠지는데 이 침하량가지 전술의 방법으로 예측하는 것은 무리가 있기 때문에 한계하중을 재하할 경우의 삼차원 압밀침하량의 산정은 극히 어렵다.

삼차원적인 압밀침하의 시간경과를 구하는 이론은 1941∼1957년의 Biot의 연구가 가장 유명하다. 이 연구의 삼차원탄성체의 입장에서 유도된 압밀의 기본식은 다음과 같다.

위의 두식은 약간의 차이가 있는데 이들의 식은 각종 조건에 대하여 해를 구하며, 그 형태가 복잡하기 때문에 현재의 경우 일반적으로 사용되고 있는 것은 거의 없다.

Terzaghi 계열의 이론을 샌드드레인의 경우에 이차원압밀로서 구한 Barron의 이론이 예외의 경우이고, 일반적으로는 Terzaghi의 일차원압밀 과정을 다소 수정하여 사용하고 있는 정도이다. 예를 들면 Skempton의 연구에서도 Si가 t=0의 순간에 발생하고 그 후 Sc는 Terzaghidm 일차원이론 그대로 적용하고 있다.

압밀이론에 의하여 구조물 침하를 해석하는 입장에서 보면, 압밀이론의 삼차원화 외에도 점토의 압밀특성과 이차압밀이라 칭하는 레올로지적 침하, 여기에 이러한 것을 추가한 의미에서의 침하에 관한 상사법칙 등 해결해야 할 문제가 많이 있어 상당히 복잡하다.