62. 압력구근(pressure bulb) |
|
||
|
|
|
|
|
|
|
지표면에 연직인 집중하중 Q 가 작용할 때 지반 내부에 생기는 응력은 기초구조 설계시에 매우 중요한 인자이다. 이것은 지반은 반 무한의 탄성체로 가정하여 그 표면에 연직 집중하중 Q 가 작용할 때에 탄성체 내에 생기는 응력을 구하는 방법으로서 Boussinesq에 의한 해법의 예를 들면 식(1)과 같다.
기타의 기호는 그림 62-1을 참조하기 바란다.
식 (1)은 점토지반에서는 실험결과와 비교적 잘 일치하지만 모래지반에서는 잘 일치하지 않으며, 하중의 작용점 아래에 응력이 집중하는 경향이 있다. Frohlich 는 하중의 작용점에서 응력이 방사상으로 직진한다고 가정하여 식 (1)을 수정하여 식 (2)를 제안하였다.
여기서 ν ; 집중계수 (1,2,ㆍㆍㆍ등의 정수) 식 (1)에서 μ = 1/2 로 하면 식 (2)에서 ν = 3의 경우와 같으며, 또한 σz는 포아슨비 μ와 관계가 없으므로 ν=3 이면 식 (1)과 식 (2)는 같다. 하중작용점 직하에서 지표면에서의 심도 Zo의 응력은 식 (3)과 같다.
지표면에서 심도 Zo 범위 내의 σzo 와 같은 값의 응력이 생기는 지중의 점은 식 (4)와 같다.
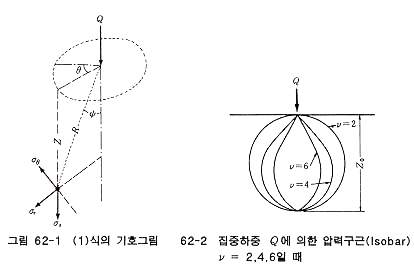
식 (4)의 궤적을 Isobar 라 부르며, 그림 62-2와 같은 형상이 되는데 Isobar로 주어지는 점의 응력은 지표면으로부터의 심도에 관계없이 일정한 값을 나타낸다.
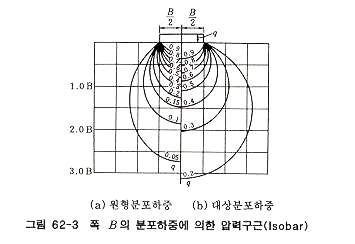
지표면에 원형 및 띠상의 연직분포하중 q가 작용할 때 지반 내부에 생기는 응력은 식 91)을 응용하여 구할 수 있다. 이 때도 식 (4)와 같이 σz가 일정한 점을 연결하여 얻어지는 곡선, 즉 Isobar를 구할 수 있는데 일반적으로 σz를 q 값에 대한 비율로 나타내며 그림 62-3과 같은 형태로 된다. 그림62-2 및 그림 62-3에 의하여 규명된 바와 같이 σz의 값이 일정한 위치를 나타내는 Isobar의 형태는 식물의 구근과 유사하므로 Isobar를 압력구근이라 부르는 경우도 있다. 압력구근 내부으 지반은 외부에 비하여 큰 응력을 받으므로 기초설계시는 이부분 흙의 성질을 충분히 조사해야 한다. 그림 62-3에서 지중응력이 지표면하중의 2/10 값이 되는 심도는 원형분포하중일 때 하중 폭의 1∼1.5배이며, 띠상분포하중은 그 배 이상의 심도가 된다. 따라서 기초설계시는 기초횡 폭 비율에 따라서 조사해야 할 지반의 심도를 결정해야 한다. 모래지반 아래에 연약점토층이 있을 경우 그림 62-4와 같이 폭이 작은 재하판으로 재하시험을 하면 압력구근이 모래층 내부에만 형성되고 점토층까지 도달하지 않는다. 한편 건물은 기초 폭이 크므로 같은 응력의 압력구근이 점토층 내부까지 형성되는 경우가 많기 때문에 이러한 경우에 폭이 작은 재하판으로 시험을 하면 그 결과를 기초 폭이 큰 건물설계에는 쓸모가 없게 된다. |
|
|
|
|
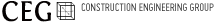
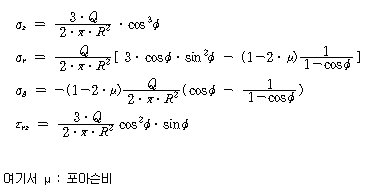 (1)
(1)
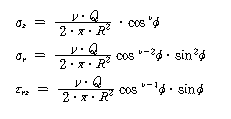 (2)
(2)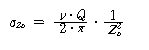 (3)
(3)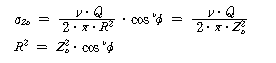 (4)
(4)