64. 압밀도(degree of consolidation)

   가. 정의

 지반의 투수성이 작기 때문에 하중을 받은 점성토지반의 침하는 대부분 시간적으로 지연 발생한다. 이같은 현상을 표시하는 방법으로 압밀도가 사용된다. 여기서는 포화점성토지반을 대상으로 압밀도를 생각해 보기로 한다. 먼저 침하에 대한 압밀도 up는

                                           (1)

로 정의하는 것이 보통이다. 지반이 포화되어 있는 경우에는 즉시 침하가 전단변형만에 기인하고 압밀배수에 직접적 관계를 갖는 체적 변형에는 관계치 않는다.

이 때문에 즉시침하를 압밀과정에서 제외하고 배수에 따른 침하만을 압밀도로 정의하고 있다. 침하가 압밀에 대한 종합적 지표인데 대하여 지반 내 임의점에서 압밀상황의 지표는 체적변형이다. 체적변형에 대한 압밀도 ue는 식 (2)로 정의 된다.

                               (2)

이 정의는 침하에 대한 압밀도의 정의와 같다.

포화점성토지반에서 흙입자와 간극수는 비압축성으로 볼 수 있으므로 순간적인 체적변형은 발생하지 않는 것으로 생각된다.

   나. 압밀도와 간극수압

 점성토 지반에 재하하면 간극수압이 발생하며, 그의 소산과정이 압밀진행과정에 해당되는데 Terzaghi 의 1차원 압밀이나 Barron의 샌드드레인에 의한 압밀에서는 함께 체적변형에 대한 압밀도 ue는 식 (30으로, 침하에 대한 압밀도 up는 식 (4)로 정의할 수 있다.

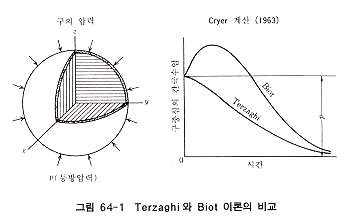
이를 보면 확실히 압밀진행과정과 간극수압의 소산과정이 1:1로 대응하고 있다. 이같이 압밀도와 간극수압의 직접적인 대응은 어느 경우에도 존재하는지는 Terzaghi 가 일차원 압밀이론을 발표한 이후 계속 문제되었으며, 이에 대한 해답은 Cryer 가 주고 있다(그림 64-1 참조).

Cryer 는 Terzaghi와 Biot의 압밀이론을 비교하기 위하여 공(구)형태의 점토에 대하여 등방압,외주면 배수조건을 기초로 양 이론의 해를 구했다. 그런데 구의 중심에서 간극수압의 거동이 서로 차이가 있는 것을 나타냈다. 구에 등방압 p를 가하면 구 전체에 uo = p의 초기간극수압이 발생한다. 이 점은 양 이론이 같다. Terzaghi 이론에 따르면 그 후 배수를 시작하면 구 중심의 간극수압은 압밀진행과 함께 uo = p의 초기치에서 단조롭게 감소하는데 대하여 Biot 이론에서는 일단 증가하고 어는 mrcl에 도달한 후 감소가 시작된다. 이 현상은 당시 기이하게 느껴져 Gibson은 실험에 의해 이 현상의 존재를 확인했다. 결론적으로 구의 문제는 Biot 이론을 따라야만 된다는 것이 인정되었다. 그래서 정하중에서 압밀진행에 따라 간극수압이 상승하는 현상을 발견한 사람의 이름을 따서 Mandel-Cryer 효과라 부르고 있다.

이 경우 간극수압은 초기치보다 크게 되며 점토의 구 중심을 향하여 물이 흐르는 것은 아니므로 점토구의 중심부분이 팽윤되었다고 할 수 없기 때문에 uo < u 일 때 부(-)의 압밀도를 나타내는 식 (3)은 구의 압밀에 있어서는 적당하지 않다는 것을 알 수 있다. 즉, 체적변형에 대한 압밀도가 식 (3)으로 정의 할 수 있는 것은 문자대로 간극수압의 변화량이 체적변화량에 비례하는 경우 즉, 열전도형 압밀방정식인 식 (5)가 성립하는 경우에 한정된다.

              (5)

구체적으로 말하면 샌드드레인의 유무에 관계없이 점토층이 1차원적으로 압축(Ko 압밀이라 함)되는 경우이다.

침하에 대한 압밀도 up와 평균간극수압 a의 관계식 (4)는 식 (30이 성립하는 Ko 압밀인 경우에 성립하며, 식 (3)이 인정되지 않는 구의 경우에도 인정되므로 그의 적용범위가 넓다.

그런데 식 (4)가 인정되는 것은 초기 간극수압 uo가 점토층 전체에 일정하게 발생하고 하중이 시간에 따라 변동하지 않는 경우이며, 식 (4)가 적용되지 않는 것은 띠기초나 원형기초 등 일반적으로 3차원 압밀인 경우이다. 식 (3)이나 식 94)가 적용되지 않는 경우에 압밀도는 간극수압의 거동과 관계가 없는 것은 아니나 그렇게 단순하지는 않다.

지금까지 압밀도와 간극수압에 관한 논의는 점토골조의 응력-변형관계가 직선적(선형탄성)으로 볼 수 없다는 의견이어서 점토를 선형탄성체가 아니라고 보면 식 (3) 및 (4)는 성립하지 않는다.

그래서 압밀도와 간극수압의 관계는 상당히 복잡하여 1차원 압밀에 있어서도 점토의 응력-변형 관계로서 e-p는 직선(선형)이 아니며, e-log p를 직선(비선형)으로 보면 점토가 연약할수록 또한 하중증가율이 클수록 침하가 선행하고 간극수압이 늦게 소산한다. 실제 점토를 이 이외에 소성적이라든가 다이레이턴시 특성을 가지고 있다. 이 때문에 현장에서의 압밀도와 간극수압의 관계는 선형탄성압밀이론이 나타날수록 정연하지 않다.

   다. 현장 압밀침하와 압밀도

 현장에서 압밀진행 상황은 주로 침하관측자료를 토대로 판단하며 압밀도로 표시된다. 그 때 식(1)을 사용하여 압밀도를 표시할 경우에는 2가지 문제가 있다.

첫째는 현장에서의 재하는 일반적으로 부분적이고 어느 정도의 즉시침하가 생긴다. 그러나 재하가 점증적으로 되기 때문에 즉시침하 po와 압밀침하 p의 구별이 쉽지 않은 경우가 많다. 둘째로 최종침하 pf은 앞으로 관측되는 값인데 압밀도를 표시하기 위해서는 어느 방법으로든 즉시침하량과 최종침하량을 결정해야 한다.

현장에서는 통상 그때까지의 관측침하곡선에 어느 이론 압밀침하곡선(예를 들면 Terzaghi 나 Barron 의 해 등)을 그려 즉시침하량이나 최종침하량을 결정한다.

또 경우에 따라서 즉시침하는 발생하지 않고 침하 모두를 압밀침하로 보는 경우도 있다. 이같은 방법으로 추정한 값은 문자 그래로 즉시침하나 최종침하는 아니며, 약속에 따라 얻어지는 가정치, 해석에 사용되는 압밀이론이나 해석방법에 의해 변하는 값이다. 이러한 사정은 표준압밀시험 해석에서도 마찬가지이다. 따라서 현장에서의 압밀도는 식 (1)을 정의할 때의 과정과 많은 차이가 있게 되며, 이들 값의 이용이나 해석에 있어서 주의를 요한다.