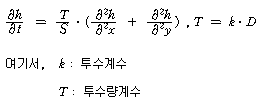84. 저류계수(storage cofficient)

  가. 정의

 "저류계수란 평면 2차원 지하수를 고려할 때 단위 수평단면적을 갖는 연직 흙기둥에서 단위 지하수위의 변화가 생길 때 발생하는 저류수 변화량의 절대치를 말한다." 라고 정의할 수 있으며, 저류계수의 기호는 일반적으로 S로 표시하고 차원은 무차원이다.

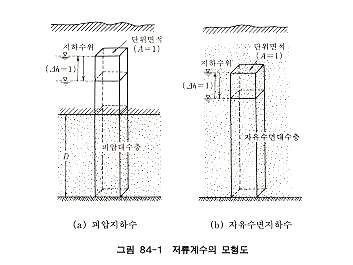
여기서 정의된 의미를 간단히 설명하면 평면2차원 지하수란 수평방향(x, y 좌표)의 변화만을 생각하고 연직방향(z 좌표)의 변화를 고려하지 않는 경우의 지하수를 말한다. 따라서 Dupuit 의 가정이 성립한다고 생각하는 경우라 해도 좋다. 그림 84-1을 참조하여 어느 수평단면을 절단해도 같은 단위면적을 갖는 지하수중의 연직기둥을 생각한다. 이 흙기둥의 모든 점에서 단위 1의 지하수위 변화(저하 또는 상승)가 생긴 경우 그 흙기둥에서 배출 또는 흡입되는 수량(즉 그 흙기둥 내 저류수의 증감량)을 나타내는 것이 저류계수이다.

  나. 물리적 의미

 대수층 상태에 따라 지하수를 피압지하수와 자유수면을 같는 지하수로 나눌 수 있으며 그 상태에 따라 저류계수의 물리적 의미가 다르다.

1) 피압지하수(그림 84-1(a) 참조)

대수층 상부의 가압층에서 물의 출입이 없는 것으로 하면, 지하수위의 변화에 따른 저류계수의 변화는 수압 증감에 따른 대수층의 신축 및 흙입자와 물의 팽창수축에 의해 초래되는 저류계수는 다음 식으로 표시된다.

               (1)

일반적으로 대수층 두께의 압축율에 비하여 물의 압축율은 아주 작으므로 (α>>β), 저류계수는 근사적으로 지하수위 변화에 기인하는 대수층 두께의 신축량으로 보아도 좋다. 비저류계수의 대표적인 값은 Domenico 에 의하면 표84-1과 같다.

표 84-1 토질과 비저류계수의 관계

2) 자유수면을 같는 지하수(그림 84-1(b) 참조)

자유수면을 갖는 지하수위 변화는 수면의 변화로 되어 나타난다. 따라서 지하수면의 상하에 따라서 그 변동영역의 간극 중 물이 출입하게 되며, 그 때 저류수의 변화량은 유효간극율 ne와 같다. 이 경우에는 앞서 기술한 피압지하수인 경우와 같이 대수층의 신축과 간극 자체에서 2종류의 저류변화가 생기게 되며, 저류계수는 다음과 같이 표시된다.

여기서, S_y 는 비산출율(Specific yield)로서 단위체적의 포화 흙덩이 중에서 중력배수되는 수량을 표시하고 유효간극율과 동일한 물리적 의미를 같는 것이다. 일반적으로 자유수면을 같는 대수층에서는 식 (2)의 우변 2항은 무시할 수 있을 정도로 작은 것으로 실용적으로는 S=Sy로 해석하여도 별차이가 없다. 이 경우 저류계수 값은 (10-2 ∼ 10-1)의 차원으로 되는 경우가 많다.

3) 기타

지하수를 피압지하수와 자유수면을 같는 지하수로 나누는 것은 편의적인 것으로 그 중간적인 것도 당연히 존재한다. 즉 피압지하수 대수층 상부의 불투수층이 완전하지 않은 경우9반투수층이라 함)가 있다.

이 같은 경우에 저류게수의 의미는 S=S_s X D 와 S=S_y 가 동승된 것이라는 해석이 옳다. 지사수위가 크게 변동하는 경우, 어는 시점(대수층)에 피압지하수가 있어 지하수위가 저하하여 자유수면지하수로 변하는 경우에 저류계수의 의미는 S= S_s X D에서 S=S_y로 변하므로 저류계수의 값도 크게 변한다.

또 지하수면이 상승(침윤)과정에 있을 때와 하강(배수)과정에 있을 때에는 저류계수가 다른 경우가 많다. 이는 자유수면 지하수의 S=S)y=n_e의 해석에 있어서 흙속에 간극수가 배제되는 경우와 간극 중에 침입하는 경우에는 모세관 현상 등에 의해 수량적으로 다르기 때문이다.

  다. 측정방법과 의의

 저류계수는 현지에서는 일반적으로 양수시험의 비정상 해석으로 산정되며, 회복법으로는 구해지지 않는다. 그 해석방법에는 Theis 방법, Jacob 방법 등이 잘 알려져 있다.

Theis & Jacob의 해석방법은 저류계수의 산정에서 몇가지의 가정을 전제로 하고 있다. ① 대수층 두께가 일정할 것 ② 저류계수는 대상영역 내에서 일정치를 취할 것 ③ 또 그것은 시간과 관계치 않을 것 ④ 지하수 함양량(강우침투 등)이 없을 것 등이다.

이들의 가정과 산출된 저류계수 또는 현실적 의미에 대하여 고려해 보면, ① 의 가정은 저류계수 산정시에, 자유수면지하수는 대수층 두께에 대한 지하수면 변동량의 비에 상당하는 오차가 필연적으로 생길 가능성이 있다. ② 는 평면적으로 떨어진 지점에는 당연히 대수층의 구조가 다르므로 저류계수의 값에도 차가 있다. 따라서 그들의 평균값을 산출하게 된다. ③ 은 저류계수의 물리적인 의미를 이해하면 알 수 있듯이 흙기둥에서의 저류수 배출, 침윤에는 시간이 걸린다. 그 시간적 지연이 무시될 정도로 빨리 배출, 침윤 시에는 문제가 없으나 점성토와 같이 침투성이 작은 경우에는 연직방향의 침출시간을 무시할 수 없다. 이 경우에 S는 시간과 함께 변하는 것은 당연하다. Boulton 과 Stallmann은 그 배출시간의 지연을 고려한 해석을 하였다.(Delayed Effedt). ④ Theis 과 Jacob의 방법에서는 지하수 함양을 고려한 해석방법이므로 현실적으로 함양이 존재하는 곳에는 산출된 S 치에 그것이 반영된다. 즉 수위저하시의 양수시험 중에 함양이 생기면 그 만큼 S 치가 큰 값이 된다.

왜냐하면 양수하여 함양이 생기면 그만큼 작은 지하수위 저하량이 관측되기 때문이다. 이같은 함양을 가진 대수층에서의 양수시험 해석에는 Hantush의 해석법 등이 있다. ①∼④의 가정이 실제로 만족하지 않는 대수층에 대하여는 Theis 및 Jacob 의 해석도상에 표준적인 곡선 또는 직선에서 벗어나는 형으로 나타나는 경우가 많다. 이들의 판독에 대하여는 현실적인 문제로서 어려운 점이 많으며 대수층의 특성을 아는데 적절한 해독이 중요하다.

저류계수는 지하수위의 시간적 변도, 즉 지하수위 변화의 전파에 큰 의미를 갖는다. 연직침투가 없는 평면 2차원 지하수에서는 시간 t 에 대한 기본식은 다음과 같이 표시된다.

따라서, (T/S)가 대단히 중요한 인자로 되는 것을 알 수 있으며, (T/S) 치가 크든(작든), 즉 T가 크거나(작거나) 또는 S가 작거나(크거나) 하면 지하수위 변동의 전파가 빠르게 (느리게)되는 것이 이해된다.

저류계수와 투수계수를 대수층 정수라 부르는 것이며, 식 (3)에서도 알 수 있는 바와 같이 지하수 변동에 가장 중요한 정수이다.