87. 점탄성(viscoelasticity)

 탄성과 점성 양쪽의 성질이 현저하게 나타나는 물체를 점탄성체라 한다. 여기서 탄성과 점성은 각각 Hooke의 탄성법칙과 Newton의 점성법칙을 따르는 성질이며, 단적으로 고체와 액체의 성질이라 보아도 좋다.

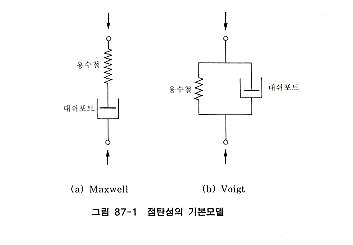
탄성을 나타내는 스프링과 점성을 나타내는 대쉬포트(dash pot)를 조합한 그림 87-1은 점탄성체의 가장 간단한 기본 모델이며, 예를 들면 껌과 비닐끈의 역학적 거동은 이들 모델로서도 충분히 나타낼 수 있다.

그러나 흙을 포함하는 보통의 물질은 여러 가지 복잡한 성질을 가지고 있으므로 스프링과 대쉬포트의 조합을 다양하게 변화시키지 않으면 응력-변형-시간의 거동을 설명하기 어렵다.

앞서 점탄성체는 고체와 액체의 성질을 겸한 물체라고 설명하였는데 포화토에서는 고상과 액상으로 구성되어 있으므로 점탄성체라 할 수 있다. 그러나 한마디로 고체, 액체라 해도 문제는 간단히 해결되지 않는다.

예를 들면 수면을 강타하면 그 순간 물은 단단한 판과 같이 느껴지며, 암석도 장기간에 걸쳐 힘을 가하면 물엿과 같이 흐른다. 결국 외력을 가하는 시간의 장단에 따라서 액체가 마치 고체와 같이 거동하고 또한 반대의 경우도 있으므로 여기에 완화시간(relaxation time)의 개념이 등장한다.

물질은 각각 고유의 완화시간이 존재한다고 생각된다. 완화시간은 그 물체가 탄성을 잃어서 유동되는 여부의 시간척도를 나타내는 것인데 알기 쉽게 말하면 힘을 가하고부터 소멸되기까지의 시간이다.

이와 같이 완화시간을 도입하면 완화시간이 무한대인 물질은 완전한 고체이고, 영인 것은 완전한 액체라고 말 할 수 있으며, 여기서 점탄성체의 완화시간은 영과 무한대의 중간이다.

하나의 예를 들면 아스팔트는 전형적인 점탄성체이지만 이를 말뚝의 부마찰력을 제거하기 위해 말뚝주면에 도포한 말뚝의 타입으로 충격력을 받을 때 아스팔트의 거동은 탄성적이다.

그러나 주변지반의 침하는 아스팔트의 완화시간을 휠씬 넘어서 조금씩 진행하므로 점성(액체)거동을 나타내며, 지반과 말뚝 사이의 마찰을 저감하는 효과를 기대할 수 있다.

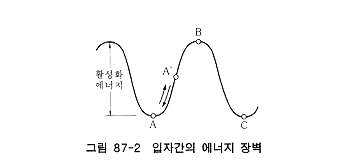
다음에 관점을 약간 바꿔 점탄성을 미시적으로 보아서 그림 87-2는 2개의 입자 사이에 존재하는 에너지의 장벽을 모형적으로 나타낸 것이다. 그림 중의 A와 C가 입자(원자 및 분자)의 위치이며, 이들이 자신의 위치를 이탈하여 이동하려면 B에 나타낸 에너지의 산을 넘어야 한다.

A에서 C로 이동(유동)시 고체의 입자는 서로 강결합(에너지 장벽의 높이)으로 되어 있어 외력을 가하거나 온도를 높이지 않으면 그 산을 넘을수가 없다.

즉, 온도를 높이면 A위치에 있는 입자는 열진동을 하게 되며, 그 진동수는(보그쯔만정수) X (절대온도)/(프랭크정수)로 된다. 따라서 온도가 높아지면 입자의 진동은 매우 심해져 에너지의 산을 자유로 넘어서 C의 위치로 이동할 수 있게 되며, 이때 고체는 녹아서 액체로 된다.

그림 87-2에서 외력을 가하면 A의 입자가 A'의 위치까지 상승하고 이 상태에서 힘을 제거하면 다시 원위치 A까지 되돌아 오는데 이것을 탄성이라 한다.

그런데 에너지의 산이 낮으면 A'까지 올라간 입자가 자신의 열운동으로 산을 넘어서 C로 이동하는 입자도 있는데 이것이 점성을 나타나게 된다.

같은 물질 중에서 산의 높이가 불균일하게 분포되어 있는 경우는 같은 크기의 외력에 대해서 넘을 수 있는 산과 넘을 수 없는 산이 나타난다. 즉 점성과 탄성을 겸비한 점탄성체는 이와 같이도 설명할 수 있는 것이다.