
2. 간극수압계수(pore pressure coefficient) |
|
|
|
|
|
|
|
간극압의 변화를 외압 변화량의 함수로서 나타낸 형태의 계수를 간극수압계수라 한다. 이 간극압게수의 고려를 최초로 주장한 사람은 Skempton으로 비배수 삼축압축시험에 있어 축압 Δσ1, 측압 Δσ3 의 변화에 의한 간극압 변화 Δu를 다음과 같이 표시하였다.
이 식에서 A와 B를 Skempton의 간극압계수라 부르고 있다. 윗 식은 등방적인 압력변화에 의한 간극압 변화 B Δσ3와 전단응력 변화에 의한 간극압변화 B A (Δσ1-Δσ3) 로 나누어 나누어 고려하고 있다. 흙입자 골격을 탄성으로 가정하면, 삼축압축시험에 의한 A = 1/3, 평면변형 조건의 압축에서는 1/2이 된다. 계수 B 는 흙이 포화되어 있다면 항상 B = 1.0 이고, 포화도의 감소와 함께 갑싱 작아진다. 지금까지 간극압계수의 검토는 대부분 포화토를 대상으로 한 것이기 때문에 간극압계수라 하면 포화토의 간극수압계수 A를 의미하는 경우가 많다. A의 값은 전단과정에서 변화하지만, 전단시험에서 파괴시에 대응하는 값으로 하는 것이 보통이다. 이 A의 값은 흙의 조성이 점성토에서 사질토로 변화함에 따라 감소하고 점성토는 과압밀비가 클 수로 적어진다. 정규압밀점토에서는 Af = 0.5 - 1.0, 모래에서는 Af < 0 이지만 밀도가 크면 그 값은 감소한다. 그 후 Skempton은 3주응력상태에 대하여 위의 식을 확장하여, 체적변화에 대응한느 평균 주응력 성분과 형태의 변화에 대응하는 주응력차 성분으로 나누어 다음과 같이 제안했다.
이 식에 의하면 간극압계수 a는 흙의 압축성과 다이레이턴시 특성에 의해 결정된다. 처음식은 주응력변화의 부호관계에서 삼축신장시험에서는 적용이 불가능하지만, 축압을 σa, 측압을 σr 로 하여 위의 식을
로 쓰면, 삼축압축과 삼축신장의 양시험에서 같은 계수 a가 구해진다. 는 (A-1/3)과 같다. Henkel 은 정팔면체 수직응력 와 정팔면체 전단응력 을 고려하여 다음식을 제안했다.
실제문제에 적용하는 경우는 지중응력의 분포와 간극압게수로부터 간극압변화를 산정하고, 대응하는 유효응력의 변화를 검토해야 한다. 이 경우, 연직전토피압의 변화분 Δσv 에 대하여 또는 로서 간극압의 변화분 Δu를 추정하며 이 , 도 간극압계수라 부른다. 그러난 간극압계수는 전단응력의 값에 의해 변화하는 것이기 때문에 안정문제에서 안전율의 값과 관련되나 그 적용은 곤란하다. 불포화토의 경우에는 간극공기압도 고려하기 때문에 더욱 복잡하게 되고 실험실 내에서 취급하는 자체도 상당히 곤란하다. |
|
|
|
|
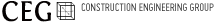
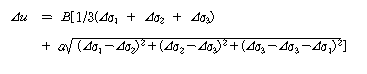 (2)
(2)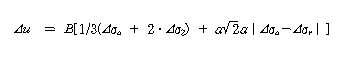 (3)
(3)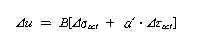 (4)
(4)