15. 다이레이턴시(Dilatancy)

 다이레이턴시의 어원은 Dilate 라고 하는 동사인데 이 동사는 "넓어지다"와 넓히다"와의 양방의 의미를 갖고 있다. 다이레이턴시는 낱알이 모여 있는 입상체의 독특한 성질롯 1885년에 Osborne Reynolds가 보고하기까지 누구도 알지 못한 것이었다.

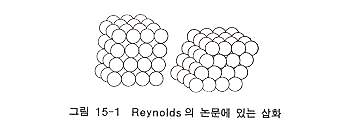
물체요소에 작용하는 전단응력에 의하여 변형되는 물체에서는 전단변형이 발생한다. 소위 연속체에서는 이 때 전단변형만을 일으키지만, 입상체에서는 이와 동시에 용적변화도 생긴다. Reynolds는 그 성질은 다이레이턴시라 명명하였고 그의 논문에서는 설명을 위하여 그림 15-1과 같이 가장 조밀, 가장 느슨한 동일한 구의 집합체를 예로 들었다. 이 집합체가 전단변형을 받으면 전자는 느슨해지고, 후자는 다져져 용적변화가 생긴다. 중간에 있는 집합체에서는 용적변화도 중간정도로 된다. 이상이 다이레이턴시의 가장 간단한 설명이다. 물체요소의 용적을 변화시키려면 사방팔방으로부터 압축하던가 누르는 압력을 감소시키면 된다. 역으로 물체요소의 용적이 변화되었을 때 이것은 사방팔방에서 작용하는 압력의 증감때문만이 아니고, 전단변형도 원인이 된다는 것이 입상체의 특징이다.

Reynolds도 그 성질이 입상체의 역학에서는 가장 기본적으로 중요한 것으로 고려했지만, 그 당시의 입상체역학에서는 Coulomb과 Rankine의 토압론과 다이레이턴시를 결합하는 것은 불가능하였다. 이것은 옛날 입상체역학에서는 Coulomb, Rankine의 전통에 따라 변형을 고려하지 아니한 활동면의 역학이었기 때문이다.

토질역학에서 다이레이턴시를 채용한 것은 Jenkin이 처음이고 그 다음에 Casagrande의 한계간극비의 제창이다. 전자는 모래의 변형에 따라 내부마찰각이 변화하는 것은 다이레이턴시에 의한 것이고, 후자에서는 전단변형에 의한 용적 팽창 수축이 있다면 간극비가 적당한 값으로 되는 때는 전단변형이 있어도 용적변형을 일으키지 아니한다고 말한 것이다.