17. 단립구조(aggregated structure)

 점토콜로이드와 같은 분산계에 전해질이 존재하면 Van Der Waals 력 및 쿨롱력 등에 의한 응집력에 의하여 점토입자의 집합체가 매우 빠르게 생기며, 점성토는 이와같이 집합체를 형성한 점토입자로 구성된다.

이 때 생기는 1차단립은 보통의 교란정도로서는 파괴되지 않으며, 점토 슬러리의 침적과정 및 압밀, 전단과정에서 2차 단립이 형성된다.

그리고, 외부의 작용력에 의하여 단순한 평형위치에서 더욱 안정된 상태로 이행하여 간다. 이러한 단립의 변형이 점성토 구조의 모델화를 의미하고 있어 점성토는 몇 개의 점토입자 집합체인 단립이라는 기본 단위가 중요하다.

흙의 구조는 "여러가지 입경을 가진 흙입자가 경계조건과 초기조건의 차이에 따라서 과거에 받은 물리적, 물리화학적 작용력의 결과로서 입자의 배열을 표시한 것"이라고 정의되며, 단립구조는 물론 이 정의의 범위 내에 있다.

종래부터 흙구조의 기본모델로서 점토입자 하나하나의 배열에 착안한 랜덤구조, 면모화구조, 분산구조, 배향구조라는 용어가 사용되어 입자의 배열 접촉을 나타내는 것으로서 면-면접촉, 면-단접촉, 단-단접촉이 있다.

이러한 단순한 구조 형태는 현실로는 거의 생기지 않으며, 약간 판상결정이 탁월한 카올리나이트 광물의 균일토층에서 보여지는 정도이다. 일반적으로 자연 점성토에서는 점토광물입자가 단립을 형성하고 있어 침강, 퇴적 및 압밀 과정에서도 이 단립입자의 거동이 중요하다.

단립입자의 측정법은 직접적 방법과 간접적 방법 두가지 방법이 있는데, 직접적인 방법은 주사형 전자현미경을 사용하여 토층단면 중의 단립을 직접 관측하여 계측하는 것이며, 간접적인 방법은 점토입자의 침강시에 슬러리 계면의 침강속도로부터 Stokes 법칙을 사용하여 응집된 단립입자 형상을 구형이라고 가정하고 산출하는 방법이다.

후자는 물론 침강시에 단립입자 지름 밖에 알 수 없으므로 역학적인 작용하에서 단립출현 상황을 파악하기 위해서는 현재의 경우 주사형 전자현미경에 의한 방법이 유일한 수단이다.

자연침강 퇴적상태에서 압밀과정의 단립출현 상황의 관찰결과에 으하면 자연 퇴적시의 모난 단립형태가 압밀이 진행됨에 따라 원체로 변화한다.

이러한 단립구조의 정량적인 표현방법으로서 단립경 분포가 있는데 단립 형상이 매우 부정형이므로 그린 지름(정방향 지름으로서 수평방향 지름과 수직방향 지름을 휘한 것)을 측정하고 있다.

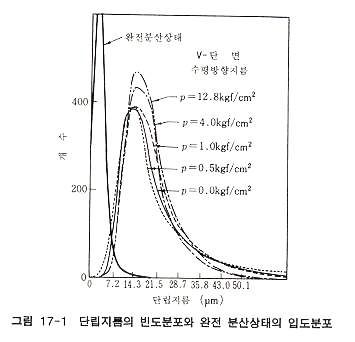
정방향 지름의 빈도 분포도를 나타낸 것이 그림 17-1인데 압밀에 의하여 수평방향의 지름이 증대된 것을 보여 준다. 여기서 단립의 평균지름 D₅₀을 취하면 10μm 정도에서 20μm 정도가 되며, 단립의 형상 특히 편평화 정도에 대해서는 수평방향 지름과 수직방향 지름의 비를 각각의 단립마다 산정하고 먼저와 같이 통계적으로 표현할 수 있다.

같은 시료를 완전 분산 상태로 하여 정방향 지름을 측정한 결과를 그림 17-1에 함께 나타내었다. 자연 퇴적시의 단립분포와는 매우 다르며, 점성토 구조가 점토입자 하나하나의 거동에 의존하는 것이 아니고, 단립으로서 취급되고 있다는 것을 명확히 나타내고 있다.

또한 점성토의 압밀에 따른 배향성에 관한 점토입자 개개의 배향 정도에 대해서는 X선회절, 기타 방법으로 구할 수 있다. 특히, X선회절을 사용한 구조 지수(fabric index) 등이 있는데, 점성토가 지닌 단립구조 때문에 압밀 중의 입자 개개의 배향성은 매우 미소하고, 완전입자배향을 취하기 위해서는 압밀압력 104 ∼ 105 kgf/cm2 이라는 막대한 하중이 필요하다고 추정되고 있다.